Rapidly-Exploring Random Tree (RRT)

14 August 2023
[ robotics ]

The Rapidly Exploring Random Tree (RRT) algorithm is a popular path planning algorithm used in robotics. It efficiently searches nonconvex, high-dimensional spaces by randomly building a space-filling tree.

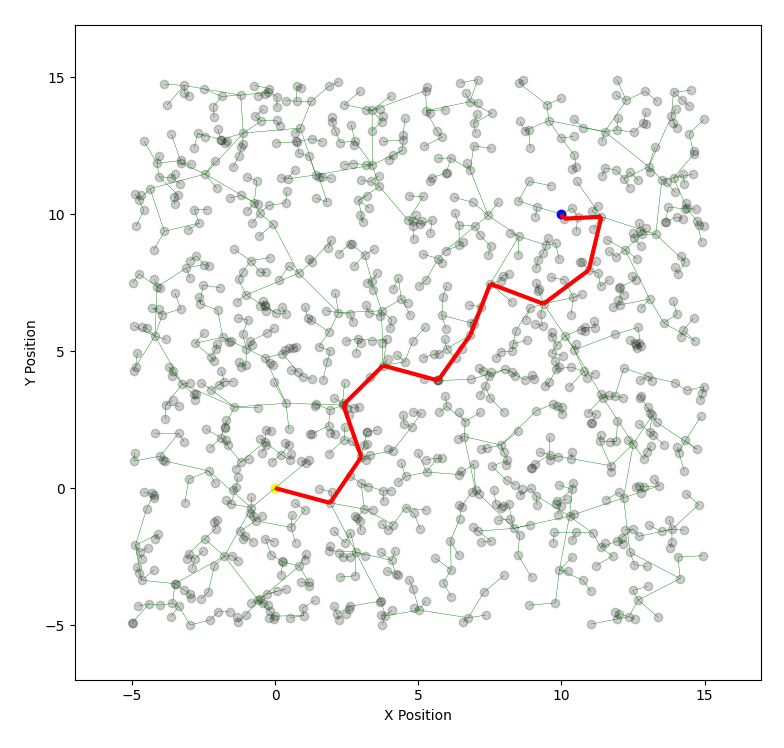
RRT Algorithms, blue point is the goal position, grey points are the vertices, edges are showed with green color and red line is the shortest path,

RRT Algorithms in 3D, with random points in the spaces

RRT* Algorithms in 3D, with less points and more optimimal path

Intialize a Graph(Vertex, Edge) with containing edges and vertices, initialized as (start_pos, end_pos).
Randomly generate points (vertex) in the space.
Check if the newly created vertex lies outside of an obstacle.
Find the nearest vertex to the closest available vertices in the tree.
Steering vertex to avoid obstacles when chaining the vertex to its closest neighbor.
Add new vertex and edge with nearest vertex into Graph
Repeat steps 1-5 until a node is generated within the goal region or a limit is reached.

Variations of the RRT algorithm have been developed to improve its performance and convergence to an optimal solution. Some notable variations include:

RRT: Rapidly-Exploring Random Tree, which is an algorithm designed to efficiently search nonconvex, high-dimensional spaces by randomly building a space-filling tree. The tree is constructed incrementally from samples drawn randomly from the search space and is inherently biased to grow towards large unsearched areas of the problem. RRTs were developed by Steven M. LaValle and James J. Kuffner Jr pdf

Snippet code of RRT in Python:

RRT.py

def RRT(startpos, endpos, n_iter, radius, stepSize, goal_radius, obstacles):
    G = Graph(startpos, endpos)
    for _ in range(n_iter):
        # 1. Sample a random Vertice
        randvex = G.randomPos()

        # 2. Check vertex inside the Obstacles (if inside -> True, otherwise: False)
        if isInObstacle(randvex, obstacles): 
            continue

        # 3. Find the near vertices
        nearvex, nearidx = nearest(G, randvex, obstacles)
        if nearvex is None:
            continue

        # 4. Steer steerVertex
        newvex = steerVertex(randvex, nearvex, stepSize)

        # 5. Add vertex and edge with nearest vertex
        newidx = G.add_vertex(newvex)
        dist = distance(newvex, nearvex)
        G.add_edge(newidx, nearidx, dist)

        #6. check if the point reach the goal
        dist = distance(newvex, G.endpos)
        if dist < 2 * goal_radius:
            endidx = G.add_vertex(G.endpos)
            G.add_edge(newidx, endidx, dist)
            G.success = True
            # print('Found Goadl!')
            # break
    end = timer()
    print("Execution time RRT:", end - start, "seconds")
    return G

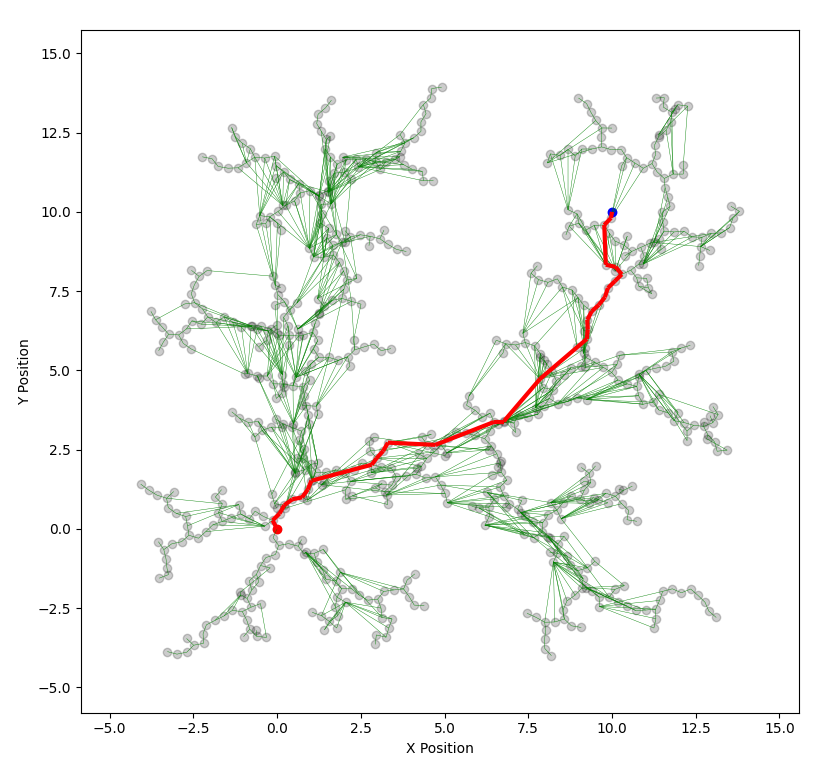
RRT: is a variant of the Rapidly Exploring Random Tree (RRT) algorithm, which is designed for efficiently searching nonconvex, high-dimensional spaces by randomly building a space-filling tree. While RRT gives a valid path but not necessarily the shortest path, RRT is an optimized version of RRT that aims to achieve a shortest path by rewiring the tree in a way that a given such radius and always tries to find a shorter path from the randomly sampled node back to the start in the tree. This makes RRT* to give an optimal solution and makes it even more feasible for high dimensional problems. RRT* is particularly suitable for path planning problems that involve obstacles and differential constraints, but it is not suitable for non-holonomic vehicles. RRT* was developed by Sertac Karaman in paper Sampling-based Algorithms for Optimal Motion Planning pdf

Snippet code of RRT* in Python:

RRT_star.py

def RRT_star(startpos, endpos, n_iter, radius, goal_radius, stepSize, obstacles):
    start = timer()
    G = Graph(startpos, endpos)

    for _ in range(n_iter):
        # 1. Sample a random Vertice
        randvex = G.randomPos()
        if isInObstacle(randvex, obstacles): #check vertex inside the Sphere Obstacles
            continue
        # 2. Find the near vertices
        nearvex, nearidx = nearest(G, randvex, obstacles)
        if nearvex is None:
            continue
        
        # 3. Steer steerVertex
        newvex = steerVertex(randvex, nearvex, stepSize)
        
        #4. Add vertex and edge with nearest vertex
        newidx = G.add_vertex(newvex)
        dist = distance(newvex, nearvex)
        G.add_edge(newidx, nearidx, dist)
        G.distances[newidx] = G.distances[nearidx] + dist

        # 5. Rewire step: update nearby vertices distance (if shorter)
        for vex in G.vertices:
            if vex == newvex:
                continue

            dist = distance(vex, newvex)
            line = Line(vex, newvex)

            if isThruObstacle(line, obstacles):
                continue

            if dist > radius:
                continue
            
            # When dist < radius implement this code
            idx = G.vex2idx[vex]
            if G.distances[newidx] + dist < G.distances[idx]:
                G.add_edge(idx, newidx, dist)
                G.distances[idx] = G.distances[newidx] + dist


        # 6. Check the goal
        dist = distance(newvex, G.endpos)  
        if dist < 2 * goal_radius:
            endidx = G.add_vertex(G.endpos)
            G.add_edge(newidx, endidx, dist)
            try:
                G.distances[endidx] = min(G.distances[endidx], G.distances[newidx]+dist)
            except:
                G.distances[endidx] = G.distances[newidx]+dist

            G.success = True
            print('success')
            break
    return G

References

Depth First Search (DFS) Explained: Algorithm, Examples, and Code link
Depth First Search Wiki link
Depth First Search (DFS) in Python link
Udemy course the introduction sampling based motion planning algorithms link
TreeNode - Nonlinear Data Structure Link
Useful Python Implementation of Rapidly-exploring random tree (RRT) Path-planning Algorithm from Fanjin Zeng link