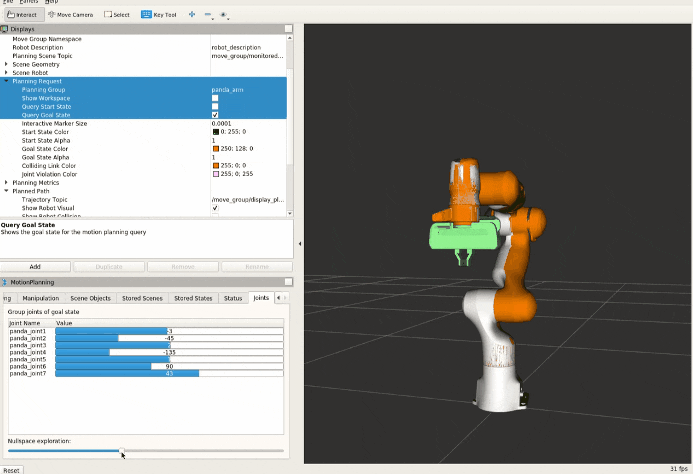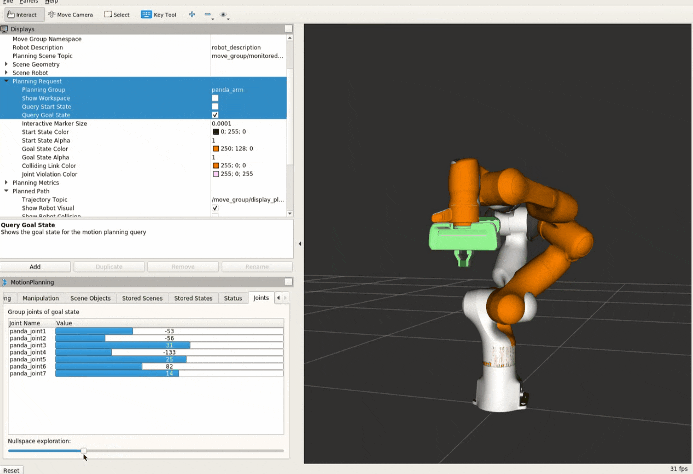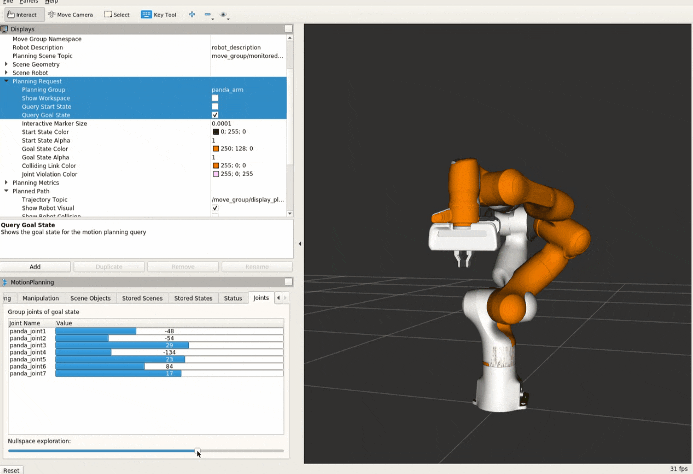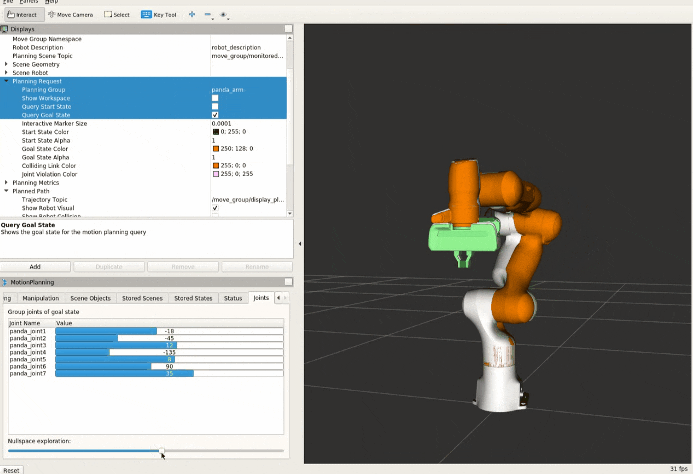
The Null space motion in the context of robotics and linear algebra, refers to the motion of a robotic manipulator within the null space of its Jacobian matrix. The null space of a matrix is the set of all vectors that the matrix maps to the zero vector. In the context of robotics, the null space of the Jacobian is the set of joint velocity vectors that yield zero linear and angular velocities of the end-effector. This concept is often used to achieve both task objectives and obstacle avoidance in robotic motion control. The null space is particularly relevant for redundant manipulators, where the dimensionality of the null space is defined as n - r, and n is the number of degrees of freedom (DOF) and r is the number of operational space variables necessary to specify a task.
Example video shows the null space motion
PseudoInverse (left), Pseudoinverse with the addition of null space motion (right).
How does null-space motion help in obstacle avoidance
The use of null-space motion for obstacle avoidance in robotics has some limitations. One inherent challenge is the potential conflict between task motion and obstacle avoidance, particularly when the rest of the robot arm avoids obstacles, which may result in a trade-off between task objectives and obstacle avoidance. Additionally, existing approaches may rely on increasing the distance between the obstacles and the robot arm to avoid collisions, which can lead to suboptimal motion and potential inefficiencies. Furthermore, in cluttered environments, potential-field-based approaches, including those utilizing null-space motion, may not fully account for robot dynamics, such as the fact that robots typically move along arcs when turning, which can be critical for obstacle avoidance. Therefore, while null-space motion is a valuable tool for robotic motion control, it is important to consider these limitations and explore further research to address these challenges.
Null space control refers to the ability of a robotic manipulator to move within the null space of its Jacobian matrix, which is the set of joint velocity vectors that yield zero linear and angular velocities of the end-effector. By utilizing the null space, robots can perform additional tasks or avoid obstacles while carrying out their primary objectives. This is particularly beneficial for redundant robots, as it enables them to avoid collisions with obstacles and perform compliant motion for assembly, all while optimizing their movement to satisfy both task constraints and obstacle avoidance
Implementing null-space motion with Levenberg-Marquardt Inverse Kinematics
Implementing null-space motion with Levenberg-Marquardt Inverse Kinematics (LM IK) involves several steps. Based on the available search results, I will provide a general outline for integrating null-space motion with LM IK for robotic control.
Initialize the robot’s kinematic model and the Jacobian matrix: Construct the robot’s kinematic model and calculate the Jacobian matrix for the desired configuration.
Compute the Jacobian matrix for the robot’s current configuration: Update the Jacobian matrix based on the current robot configuration.
Compute the null space of the Jacobian matrix: Use singular value decomposition (SVD) to find the null space of the Jacobian matrix.
Define the primary task and its associated control law: Specify the task constraints, such as end-effector motion or object manipulation, and the corresponding control law.
Use the Levenberg-Marquardt algorithm to solve the inverse kinematics problem for the primary task: Apply the LM IK method to find the inverse kinematics solution that satisfies the primary task constraints.
Compute the null-space motion: Utilize the null space of the Jacobian matrix to adjust the robot’s joint velocities within the null space while satisfying the primary task constraints.
Implement the null-space motion control law: Integrate the null-space motion control law into the robot’s control system to achieve coordinated motion.
Iterate the null-space motion calculation and the primary task IK solution: Continuously update the null-space motion and the primary task IK solution to achieve coordinated motion that satisfies both task constraints and obstacle avoidance.
 A minimalism robotics blog
A minimalism robotics blog